必ず解けるマインスイーパのようなパズル「宝探し」の5x5の問題

絶対解けるマインスイーパのようなパズル「宝探し」の5x5の問題です。暇つぶしにどうぞ。

			1	1
				2
			3
1		1
	2

1	2	2	2
1	1	3

	1		2	2
		3
			2
		1	1

		1
		2
1		3	2
	2
1

		1	1
		2
		2	3	2
	2

		1		1
			2
		1		1
			1	1

1	2	1
			1
			1
			1	1

		1	1
1	1	3		3
1

1
2			1
2	3	2	2

				1
			2	1
		1	2	2
1

1		2
2			1
	1
1	2

		1	2	2
	1		1
1		2

		1
2
	1	2
1
	2	3

1			1
1	2
	1	2

				1
		1	3
1		2
		2	1

必ず解けるマインスイーパのようなパズル「宝探し」の4x4の問題ができた

「宝探し」パズルの4x4ができたので問題提供します(10問)。みなさんとけますか。ルールは「マスの数字の周りにその数字の数だけ宝がある、宝のある場所を◯で埋めなさい」です。言いかえると絶対解けるマインスイーパです。それだけですが、以外に面白いと思います。ただし、2,3手先読めば解ける問題もそれ以上先読みが必要な問題もあるのでやさしくはないかもしれません。

1		1
	2		2
2		2
		2

1	2	2
2			2
2			2

		1	1
2		3
	2
	2	2

	1
2			1
1
1	2		2

		1	1
			2
1	3
1		2

	1
2	2	2
2		2
		1

		1	1
			2
	2
1	1	1

		1	1
		2
1		2
	1		1

1		2
2		4
		2
1	1

1
2			1
	3		2
	2		1

必ず解けるマインスイーパのようなパズル「宝探し」について考える

「頭がよくなる算数パズル」という本に、「宝探し」というパズルがのっていました。このパズルは解き方はマインスイーパのような感じなのですが、マインスイーパは絶対解けるとは限りませんが、このパズルは絶対解けるらしいです。早速購入してやってみたところ、マインスイーパに近い感じですが、妙に論理力を要求されます。そしてマスを数えるだけの単純な作業が意外に楽しいことに気づきました。「数独」の次は「宝探し」かなと考えて早速プログラミングです。どうやら、数字と宝を矛盾なく置くところまではできたようですがそこから先がよくわかりませんでした。どうやって作ってるのだろう、、、これから先が難しいようです。とりあえず寝て考えることにします。

頭がよくなる算数パズル: 小学3年生レベルなのに大人が苦戦する70問!

初期配置が対称になっている数独は本当に良い数独問題なのか?

パズル作家の間では数独の初期配置はきれいな対称になっているものが良いとされているらしい。私は、パズル初心者だし、パズル作家というものは最近知ったキーワードなんだが、そのような職業もあるらしく、そのような人の間では、数独の問題は対称で美しくなければならないのだそうである。個人的には、数独は対称で、かつわかりやすい形でなくてはならないという考え方には反対なのである。わたしは、数独は汚くてランダムであればあるほどよいという考え方なのである。(注意:私は数独初心者です。解いた問題数は6x6で10問くらいです。9x9に至っては解いたことがありません。そのくらい初心者の意見なのであまり参考にならないかもしれません)

なぜか

数値の入る場所を決めてから数独をつくるのは、初期配置の数値の場所を決めることがかなり強い制約なので、簡単に問題を作成することができてしまうのである。たとえば、ハート型の初期配置にしたければハートの初期配置の形にそって数値の順番を変えるだけなので、プログラム的にはそんなに難しいことではないのである。ただ、星形や四角形など人間がみて綺麗に見えるパターンを大量に作成するのは難しい気がするが。

それに、対称でない問題は汚く見えるからボツという考え方、そのものが意味を成していないのではないかとも思っています。なぜなら、対称でない問題のほうが多いと思うからです。すなわち母数が多ければそれだけ面白い問題も多いにきまってますよね。だから、母数の多い汚い問題を捨てるのはもったいないどころか、そこでしか出会えない問題もあるだろうから、パズルにさらに制約をかけて面白くない方向に力をかけているように思えるのです。

わたしには、プログラムで簡単に問題が作成できてしまう問題は、どうしても良い問題とは思えないのです。なにか、複雑なことをやってでてきた問題だけが良い問題な気がします。

もちろん、人間が熟考して作った数独問題が最高の問題だとはおもいます。

以上

どうしても解けない数独6x6ジグソーLv24問3

数独6x6ジグソーの問3がどうしても解けなかったので紹介しておきます。これ解けますか?おそらく途中で仮置きしないと解けない問題だと思います。仮置きは面倒なので思い切ってこの問題はスキップすることにします。簡単に解けたよという人はコメントください。

自作ジグソー数独のLv24の問1(難しい問題)を解いてみる

今回、自作ジグソー数独6x6の最難関に位置するLv24の問1を解きました。山場がいくつもあったので、その局面の解き方を説明します。数独やジグソー数独が解けないと悩んでいる方は、同じような山場にあたっているのかもしれませんので参考にしてみてはどうでしょうか。

まず、Lv24の問1の初期配置はこれです。

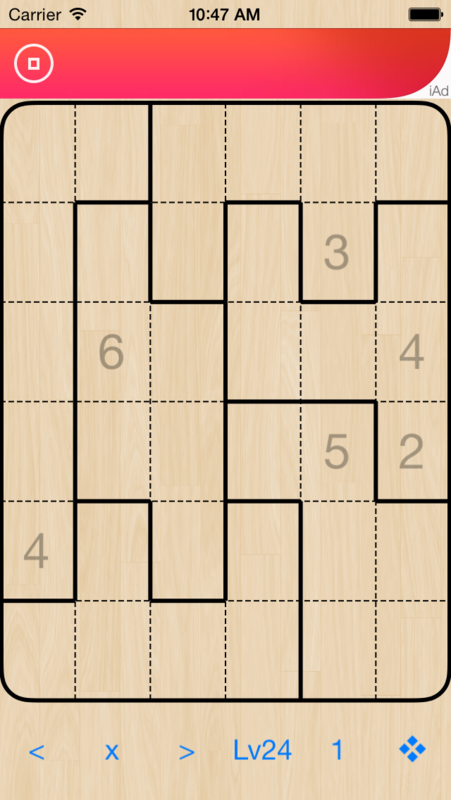
初期ヒント数は6です。ぱっと見で、3と1は以下のように埋まりました。それから次に埋められる場所がわかりませんでしたが、以下の図のようなテクニック(「未確定状態からの排他」と自分で名づけました)を使うことで4を埋めることが出来ました。

さらに、すすめていくと以下の局面になり、それも同様のテクニックで解きましたので説明のためのスクリーンショットを貼っておきます。

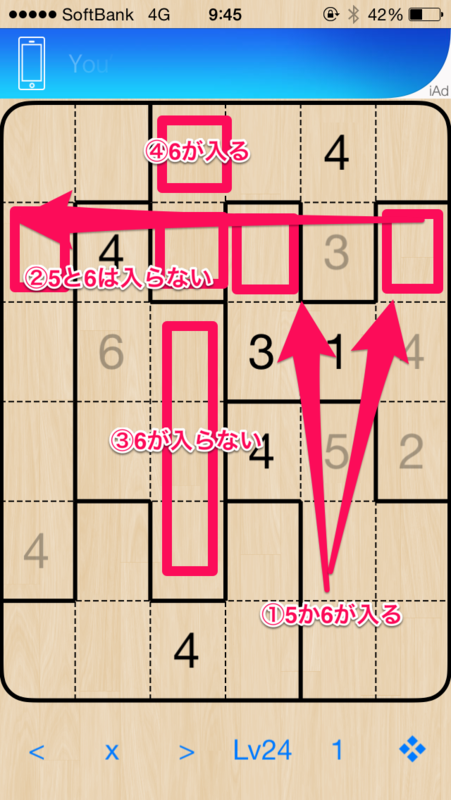
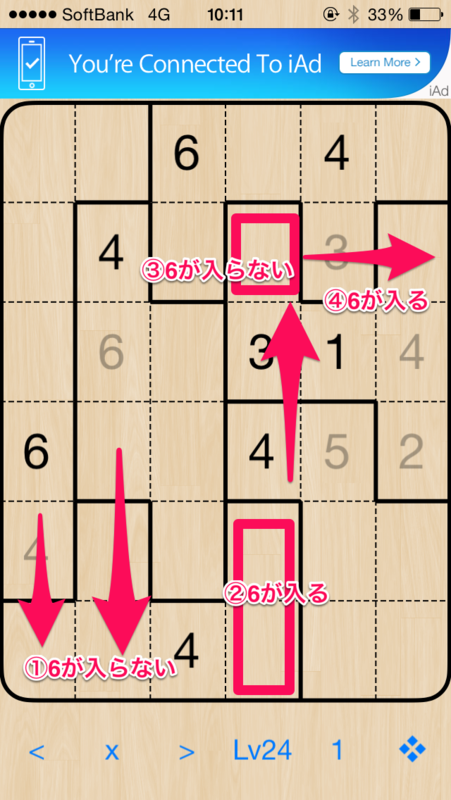
結果を見れば、「ああなるほど」とおもうのですが。「っでどこからはじめればいいの?」この理論を展開するための、スタート地点が気になるところだと思います。私の場合、どこから見ていったかというと、数字の個数です。「3が2つあるから3の制約が多い→3が確定する可能性が高い」だから3に注目して3が入る理由を考える。同じように1,2,3,4,5,6全てについて考えていきました。また、間接的なヒントを大事にしようと思ったのです。「この2マスからこの行は5,6は入らないというのは新しいヒントだな」と思ったらそれを常に心においてマス目を見ていったのです。その結果、「未確定状態からの排他」のテクニックを思いつき、そのテクニックを他の箇所にも適応することで山場をのりこえて無事すべてのマスを埋めることが出来ました。

ジグソー数独の面白い解法テクニックを発見した

自作ジグソー数独を解いていて面白い解法を見つけたので記載します。

下記図の①②③④から⑤が導き出せるのです。この山場を超えれば何とか解くことができそうです。