Pythonでドーナッツの形を描画する

いきなりですがPythonでドーナッツの形を描画します。まず、頭の中でその形をイメージします。次にそれを数式で表し、Python 3 で実装します。最後に描画されたものをみてみます。

1. 頭の中でドーナツの形をイメージする

ドーナッツの形をイメージします。以下のように円盤をz軸を中心にぐるぐる回転させると、その軌跡は、ドーナッツ形となるはずです。

回転する円盤

2. ドーナッツの形を数式で表す

ドーナッツの形を数式で表します。

以下のように、xz平面に円を定義します。媒介変数として、 u を用いると以下のように書けると思います。

xz平面の円の数式

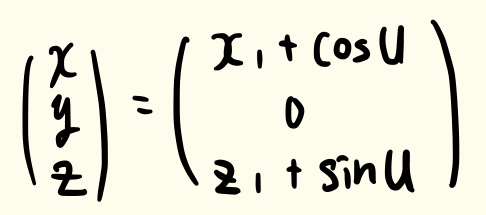
※ u は角度、x1 と z1 は座標で定数だと思ってください。円盤の半径は1とします。

この円盤を z軸 を中心に回転させます。アファイン変換*1を使うと円盤を回転させることができます。具体的には、以下の回転行列*2を上記 x, y, z の数式に作用させることになります。今回はこれを使ってやってみましょう。

回転する角度を v とすると、回転行列は以下になります。

回転行列

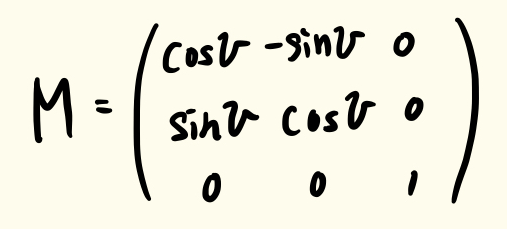
この回転行列を 先ほど定義した xz平面の円上の点 x, y, z に作用させます。回転後の円上の点を x’, y’, z’ とすると、それらの数式は以下のようになります。

回転後の数式

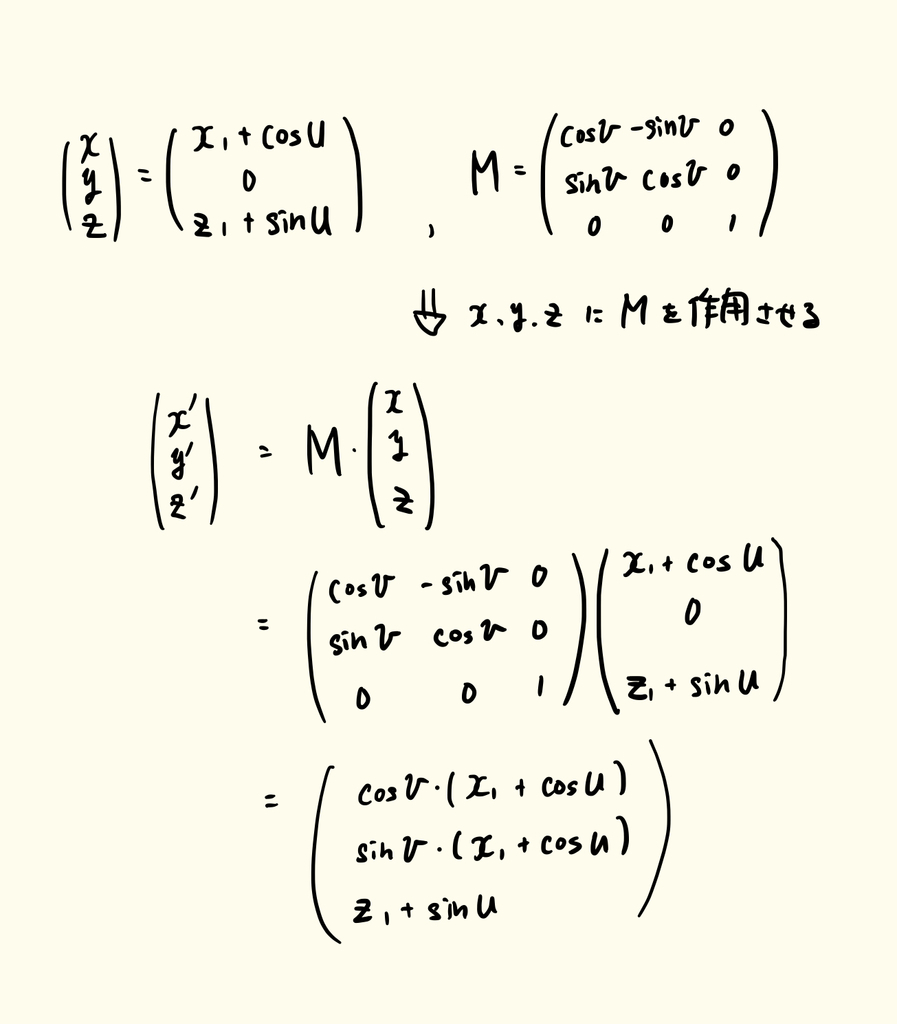
無事に、回転後の数式を変数 u, v で表すことができました。
これは u, v の２次元ですので、平面（ドーナッツの表面）を表す関数だということがわかります。
ドーナッツの形をみるのには、表面の情報があれば十分なため、この数式で十分です。

回転後の数式が求まりましたので、次は実装を行います。

3. Pythonとmatplotlibで実装する。

2.で求めたドーナッツの形を表す数式をPythonで実装しmatplotlibで描画します。
ドーナッツの形は前述の通り、 u と v で表すことができるので、この u と v を少しづつ変化させて描画すればドーナッツの形になると思われます。
注意すべき点は、描画をおこなうグラフの軸のアスペクト比率を同じにすることです。
そうしないと、目盛は正しいのだけど見た目上わかりづらいグラフになってしまいます.

コード:

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

N_us = 20
N_vs = 40

us = np.linspace(0, 2*np.pi, N_us)
vs = np.linspace(0, 2*np.pi, N_vs)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

x1 = 2
z1 = 0

for v in vs:
    x = np.cos(v)*(x1 + np.cos(us))
    y = np.sin(v)*(x1 + np.cos(us))
    z = z1 + np.sin(us)
    ax.scatter(x, y, z)

ax.set_xlim(-2, 2)
ax.set_ylim(-2, 2)
ax.set_zlim(-2, 2)
ax.set_aspect('equal')
plt.axis('off')

plt.show()

4. 描画されたものをみてみる

最後に描画されたものを見てみます。

ドーナッツ形の出力結果

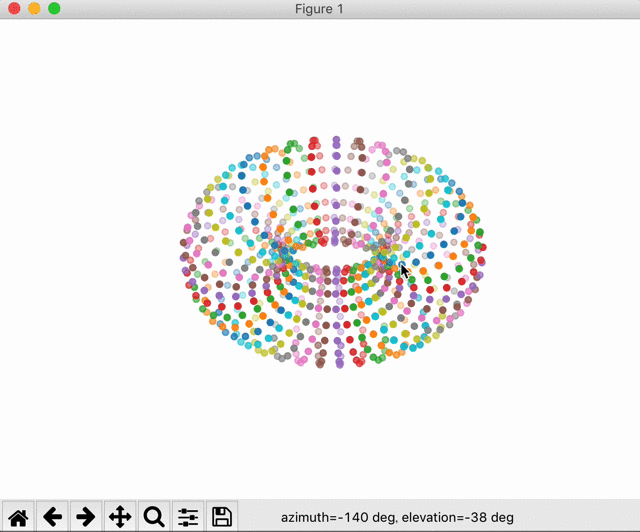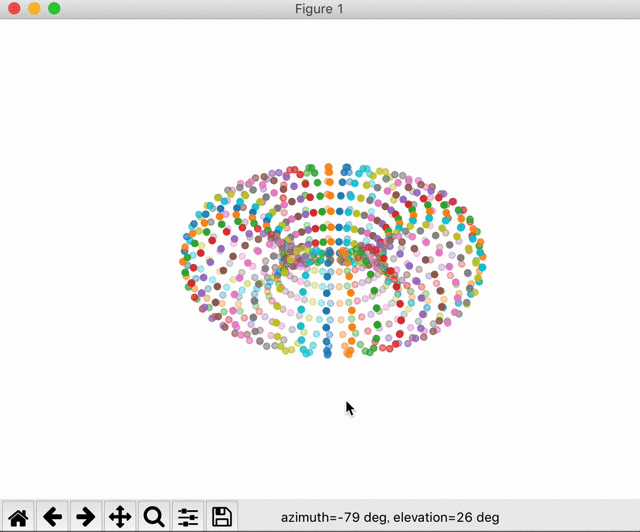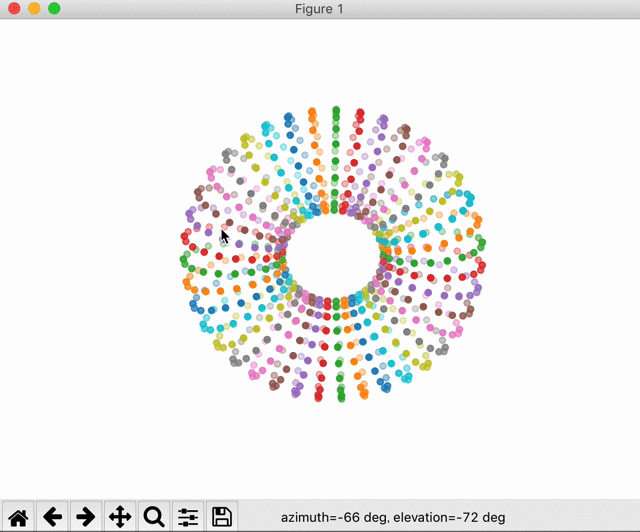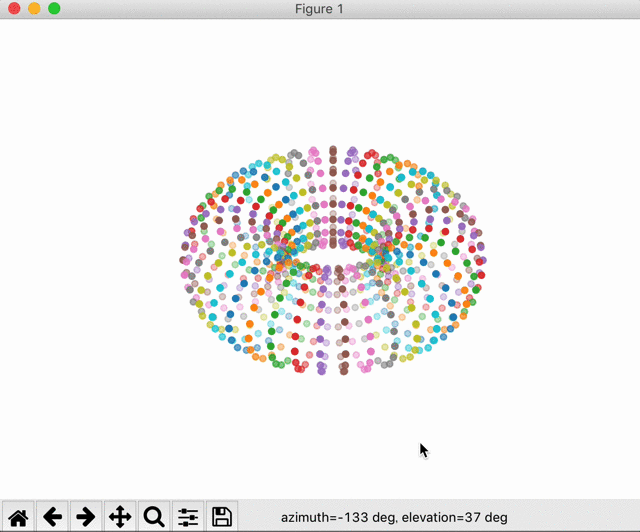
カラフルなドーナッツが表示されました。
以上です。

*1:ここでは、点を別の点に移動させるくらいの意味で使ってます。

*2: https://ja.m.wikipedia.org/wiki/回転行列

TensorFlowで複数GPUで２次元畳み込みやってみる(tf.nn.conv2d with multiple GPUs)

1. やったこと

TensorFlow の tf.nn.conv2d関数 を GCE 上でK80とV100のGPUを1個〜8個を用いて、データ並列で実行。処理速度の検証を行った。

2. わかったこと

以下のコードを試した結果、CPUのほうが３倍早く、期待はずれの結果となってしまった。こうすれば早くなるなどのコメントがありましたらぜひご教授願います。

3. PCのスペック

CPU: virtual 12 core
MEM: 32 GB
GPU: K80x8個、V100x8個で検証

4. 検証に用いたコードの概要

multi_gpu.py

GPU の数と画像データ数、画像のサイズを引数にとり、データ並列でGPUで２次元畳み込みを行い、処理時間を出力するスクリプト

run_multi_gpu.py

multi_gpu.py を GPU の数を変えて実行し結果を記録するスクリプト

5. 実際のコード

TensorFlow の 複数 GPU の使い方は公式サイトの以下のページを参考にしました。
"https://www.tensorflow.org/guide/using_gpu#using_multiple_gpus"

multi_gpu.py

import numpy as np
import tensorflow as tf
import time
import sys

N_gpus = int(sys.argv[1])
N_images = int(sys.argv[2])
width = int(sys.argv[3])
height = int(sys.argv[4])

c = []

samples = np.ones((N_images,width,height,1), dtype=np.float32)
split_samples = tf.split(samples, N_gpus, axis=0)

for n in range(N_gpus):
    d = '/gpu:%d'%n
    with tf.device(d):
        fltr = tf.constant(np.ones((3,3,1,1), dtype=np.float32))
        conv = tf.nn.conv2d(split_samples[n], fltr, (1,1,1,1), 'SAME')
    c.append(conv)
    
with tf.device('/cpu:0'):
  sum = tf.add_n(c)
  
# Creates a session with log_device_placement set to True.
sess = tf.Session(config=tf.ConfigProto(log_device_placement=True))
# Runs the op.
s = time.time()
out = sess.run(sum)
e = time.time()
print(out)
print((e-s)*1000, 'ms')


out_text = '================================================\n'
out_text = \
    'N_gpus = {}, N_images = {}, width = {}, height = {}\n'\
    .format(N_gpus, N_images, width, height)
time_estimated = '%f ms\n'%((e-s)*1000)
out_text += time_estimated

filename = 'multi_gpu_time_estimated_{}_{}_{}_{}.txt'\
    .format(N_gpus, N_images, width, height)

with open(filename, 'w') as fp:
    fp.write(out_text)

run_multi_gpu.py

# -*- coding:utf-8 -*-
import subprocess

N_GPUS_MAX = 8
python_exe = 'python3'
script_name = 'multi_gpu.py'

# データ数は GPU の個数の倍数でなければならない
# 1, 2, 3, 4, 5, 6, 7, 8 の倍数は840
# 840個の画像データ、サイズ(100,100)の
# を２次元畳み込みすることを考える

n_images = 840
width = 100
height = 100

for n_gpus in range(1, N_GPUS_MAX+1):
    command = [
    	python_exe,
    	script_name,
    	str(n_gpus),
    	str(n_images),
    	str(width),
    	str(height)]
    out = subprocess.check_output(command)
    filename = 'multi_gpus_time_log_{}_{}_{}_{}.txt'\
        .format(n_gpus, n_images, width, height)
    with open(filename, 'wb') as fp:
        fp.write(out)

6. 実行結果

以下にV100 という GPU で実行した結果を載せます。
上から順に GPU1個、GPU2個、、、GPU8個と増やして実行た結果です。

================ GPU V100 ================
N_gpus = 1, N_images = 840, width = 100, height = 100
14897.803307 ms

N_gpus = 2, N_images = 840, width = 100, height = 100
4328.074455 ms

N_gpus = 3, N_images = 840, width = 100, height = 100
5645.370483 ms

N_gpus = 4, N_images = 840, width = 100, height = 100
684.230804 ms

N_gpus = 5, N_images = 840, width = 100, height = 100
744.736195 ms

N_gpus = 6, N_images = 840, width = 100, height = 100
731.468678 ms

N_gpus = 7, N_images = 840, width = 100, height = 100
726.519346 ms

N_gpus = 8, N_images = 840, width = 100, height = 100
721.646070 ms

同様に、K80 という GPU で実行した結果を以下に載せます。

================ GPU K80 ================
N_gpus = 1, N_images = 840, width = 100, height = 100
3248.390198 ms

N_gpus = 2, N_images = 840, width = 100, height = 100
3380.734682 ms

N_gpus = 3, N_images = 840, width = 100, height = 100
3837.318182 ms

N_gpus = 4, N_images = 840, width = 100, height = 100
690.669060 ms

N_gpus = 5, N_images = 840, width = 100, height = 100
691.730976 ms

N_gpus = 6, N_images = 840, width = 100, height = 100
588.120937 ms

N_gpus = 7, N_images = 840, width = 100, height = 100
581.115961 ms

N_gpus = 8, N_images = 840, width = 100, height = 100
647.247314 ms

7. GPU がなんとなく遅い気がするのでCPUでやってみた結果

import numpy as np
import scipy
from timeit import timeit

fltr = np.ones((3,3), dtype=np.float32)
a = np.ones((100,100), dtype=np.float32)

N_images = 840

と定義して以下の scipy.signal.convolve2d で畳み込みをやってみると、、、

>>> %timeit [scipy.signal.convolve2d(a, fltr, 'same') for _ in range(N_images)]
222 ms ± 4 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

なぜかCPU1個の方がGPU8個より3倍くらい早いです。

8. GPU の使用数が 1-3 のときに遅い原因について推測してみる

GPU が 2-3 個のとき、処理時間が 1000 ms を超えており極端に遅いです。
極端に遅いケースについては、データが GPU のメモリに入りきらず、
外部とデータのやりとりを行うスワップのようなものが発生していることが考えられます。

9. CPU より GPU が遅い原因について推測、検証方法を検討してみる(検証はしません)

・TensorFlow がたいして最適されていない
⇨ Keras でも同様の結果になるか確認
⇨ Chainer など他のライブラリを使用してみる
・畳み込みのフィルタサイズの影響
⇨ フィルタサイズ 3x3 でなく10x10 などサイズを大きくする
・チャンネルのサイズの影響
⇨ チャンネルのサイズを 1 でなく 10 などサイズを大きくする
・GPUからCPUに計算結果を転送するのがボトルネックになっている
⇨ データ転送するだけのコードで検証する
⇨ GPU内でずっと計算し続けて、オーバーヘッドの影響をなくすようなコードで検証する

10. まとめ

勝手な想像ですが、 TensorFlow は tf.nn.conv2d のためにあるわけではなく、どちらかというと、ニューラルネットの重み計算を行うために最適化されているはずです。そのため、静的な数式で表されるような重み更新の計算式などはうまくGPUで分散して計算できると思うのですが、畳み込みのようなシーケンシャルな処理は単純な計算式で表現できないため、それも遅さの原因の一つかなと思います。ただ、そうはいっても今回の例ではデータ並列したはずなので、GPUの数に比例して早くなるはずだったのですが、そうはなりませんでした。現実は厳しかったです。このような畳み込みだけを行うという特殊なケースでは単純にGPUを増やせば早くなるというわけではないようですので注意が必要かと思われます。
いろいろ書きましたが、検証は面倒なので、TensorFlowの開発者が最適化をすすめて、コードを書き換えなくても自動で計算リソースをスケールしてくれる日がいつかくることを期待して、メインの機械学習のアルゴリズムについて学習をすすめて行こうと思います。

以上です。おやすみなさい。

数値をエクセルの列を表すアルファベットに変換する関数

前回の記事で、数値をエクセルの列を表すアルファベットに変換するプログラムを自作しましたが、stackoverflow でもっと良い方法を見つけたため紹介いたします。そのコードを参考に関数を作成しました。このような問題は、みんながよく考えそうなことですから、自分で考えるより検索てヒントを見つけてからコーディングすれば良かったと後悔しています。

参考にした stackoverflow の記事は以下です。
stackoverflow.com

上記 stackoverflow の記事を参考に、Python で書き直して、ゼロ始まりか1始まりなのかを指定できるように関数化しました。いっちょまえに docstring も書いてみました。

数値をエクセルの列を表すアルファベットに変換する関数:

def colname(colx, index_mode="start_from_zero"):
    '''
    Return string of colx as excel column expression
    parameters:
        colx: int
            if `index_mode="start_from_one"`,
            colx is the nunber of column index start from 1.
            Otherwise or if `index_mode="start_from_zero"`,
            colx is the nunber of column index start from 0.
            (This is the default behavior.)

    return:
        colname: str
            Return string of colx as excel column alphabets expression
    
    >>> colname(0)
    'A'
    >>> colname(25)
    'Z'
    >>> colname(25 + 1)
    'AA'
    >>> colname(26*26 + 25)
    'ZZ'
    >>> colname(1, "start_from_one")
    'A'
    >>> colname(26, "start_from_one")
    'Z'
    >>> colname(26 + 1, "start_from_one")
    'AA'
    >>> colname(26*26 + 26, "start_from_one")
    'ZZ'
    '''
    if index_mode == "start_from_zero":
        offset = 1
    elif index_mode == "start_from_one":
        offset = 0
    else:
        offset = 1
        
    alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
    colname = ""
    divend = colx + offset
    while divend > 0:
        modulo = (divend - 1) % 26
        colname = alphabet[modulo] + colname
        divend = (divend - modulo) // 26
    return colname

関数の使い方＆テスト(docstring そのままですいません):

>>> colname(0)
'A'
>>> colname(25)
'Z'
>>> colname(25 + 1)
'AA'
>>> colname(26*26 + 25)
'ZZ'
>>> colname(1, "start_from_one")
'A'
>>> colname(26, "start_from_one")
'Z'
>>> colname(26 + 1, "start_from_one")
'AA'
>>> colname(26*26 + 26, "start_from_one")
'ZZ'

計算時間については、例えば"AA"だと２回whileループを回るだけです、"AAA"だと３回、"AAAAAAAAAA"だと10回です。これは10回の演算で26**10の大きさの列番号を10演算の計算で変換できるということですから、実用上十分すぎる速さです。通常の使用ではほぼ数演算のオーダーで変換できるでしょう。コードを見ると、これ以上シンプルにできないレベルですので、これがベストアンサーだと思います。数値をエクセルの列のアルファベットの形式に変換する場合は、こちらを使いましょう。

以上です。

エクセルの列を表すアルファベットを数値に、または数値をエクセルの列を表すアルファベットに変換する話

以前の記事で、エクセルの列を表すアルファベットを数値に変換するプログラムを書いたのですが、今回は、その逆変換つまり、数値をエクセルの列を表すアルファベットに変換してみようと思います。

————————
※2018/11/15追記
数値をエクセルの列を表すアルファベットに変換する関数については こちらのに記載されているものより、処理速度、保守性においてはるかに優れたコードがあります。以下のURLに記載しましたので、数値をエクセルの列を表すアルファベットに変換する場合は以下のURLを参考にしてください。
keimina.hatenablog.jp

————————

いつも通り、プログラミング言語は Python で行います。
今回は、おもいっきり横着してメモリーを大量消費する辞書を生成して無理やりやってみます。
そして最後に、作成した関数があっているかテストします。

まず、以前のコードをおさらいです。
数値をアルファベットに変換するコードは以下のようなものでした。

def conv(alphabet):
    total = 0
    for n, i in enumerate(alphabet[::-1]):
        chr_num = ord(i.lower())
        chr_A_num = ord('a')
        total +=  (1 + chr_num - chr_A_num)* (26**n)
    return total

この関数を使用するとアルファベットと数値の対応関係が得られます。
今回はこれを利用し、４文字までのアルファベットAからZZZZをこの関数に入力し対応関係を辞書として保存します。
これにより、制限付きですが、逆関数となる辞書が求まります。
制限はアルファベット４文字までということです。
それでも約４７万列を表現できるため、実用上問題となる可能性は低いと思われます。

これをクラスで以下のようにまとめてみました。
使い方は、クラスのdocstringの使用方法の欄を参照してください。

class ExcelTool(object):
    '''
    注意:
    メモリを大量に消費するので注意してください。
    47万列までしか対応しません。
    初回インスタンス生成時に47万回計算する。そのためインスタンス生成に時間がかかる。
    インスタンスを生成した後に、変換用のメソッドを呼び出せる。

    使用方法:
    >>> # 最初に必ずインスタンスを作成する
    >>> et = ExcelTool()

    >>> # エクセルの列を表すアルファベットを数値に変換する
    >>> et.excel_alphabets_to_num("AA")
    27
    
    >>> # 数値をエクセルの列を表すアルファベットに変換する
    >>> et.num_to_excel_alphabets(27)
    27
    '''
    def __init__(self):
        from itertools import product
        self.alphabets = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ' #"".join(chr(i) for i in range(65, 91))
        # 1-4文字のアルファベット作成し、数値に変換し、逆変換用の辞書を作る
        self.map_dict = {}
        for i in range(1, 5):
            self.map_dict.update({
                self.excel_alphabets_to_num("".join(alphabet_combination)): "".join(alphabet_combination)
                for alphabet_combination in product(self.alphabets, repeat=i)})
            
    def excel_alphabets_to_num(self, alphabet_combination):
        '''
        説明:
            エクセルの列を表すアルファベットを数値に変換する関数
        引数: str
            エクセルの列を表すアルファベットの文字列(大文字小文字は関係ない)
        戻り値: int
            アルファベットに対応する数値
        '''
        total = 0
        char_A = ord('A')
        for n, i in enumerate(alphabet_combination[::-1]):
            total +=  (1 + ord(i.upper()) - char_A)* (26**n)
        return total
    
    def num_to_excel_alphabets(self, num):
        '''
        説明:
            数値をエクセルの列を表すアルファベットに変換する関数
        引数: int
            エクセルの列を表すアルファベットに変換するための数値
        戻り値: str
            引数で与えた整数値に対応するエクセルの列を表すアルファベットの文字列
            文字列は常に大文字で返す。
        '''
        return self.map_dict[num]


###################################
# 以下はテストのためのコード
###################################

# はじめにインスタンスを作成する
et = ExcelTool()

print("テスト")
print("======== 数値からアルファベット========")
print("1               =>", et.num_to_excel_alphabets(1))
print("26              =>", et.num_to_excel_alphabets(26))
print("26*26+1(677)    =>", et.num_to_excel_alphabets(26*26+1))
print("26*26+26(702)   =>", et.num_to_excel_alphabets(26*26+26))
print("26*26+26+1(703) =>", et.num_to_excel_alphabets(26*26+26+1))

print("======== アルファベットから数値========")
print("A               =>", et.excel_alphabets_to_num('A'))
print("Z               =>", et.excel_alphabets_to_num('Z'))
print("ZA              =>", et.excel_alphabets_to_num('ZA'))
print("ZZ              =>", et.excel_alphabets_to_num('ZZ'))
print("AAA             =>", et.excel_alphabets_to_num('AAA'))

以下にテストの結果を載せます。
テストの結果:

テスト
======== 数値からアルファベット========
1               => A
26              => Z
26*26+1(677)    => ZA
26*26+26(702)   => ZZ
26*26+26+1(703) => AAA
======== アルファベットから数値========
A               => 1
Z               => 26
ZA              => 677
ZZ              => 702
AAA             => 703

以上になります。

少数で表される数値の出現頻度を数えてヒストグラムを作成したいAさんの話（問題）

題名の通りの問題です。問題は以下の通りです。汚文字ですいません。

問題文では少数の最小値と最大値が-2.0と2.0で、それを8つの領域に均等に分割していますが、これは一例にしかすぎません。これら(最小値、最大値、分割数)の数字が変化しても機能するように一般化した関数を求めてほしいです。

私の解答は一番下に載せます。
関数に境界値を与えると動作が予測困難な振る舞いになりますので注意が必要です。

もっと良い方法があるよなど、コメントいただけると助かります。
10/20 追記: 一番下にライブラリを使用した簡単な方法を追し記ました。

以上。

解答例 (境界値に弱いので注意):

何が言いたいのかというと`index = int((v - A) / (B - A) * N)`の１行でこの関数は実装できると言うことです。
ただし、テストデータ 2 の検証を見ていただくと分かるように境界値に弱いですので、境界値が入力として来た場合の対策は別途行う必要があります。
境界値が来たら右に少しづらすとかで対処できるかもしれません,

# -*- coding:utf-8 -*-
import numpy as np

# 分割数
N = 8

# 下限
A = -2.0

# 上限
B = 2.0

# 均等に分割した数直線
linespace = np.linspace(A, B, N + 1)

# 数直線を表示

print("================ 数直線 ================")
print("\n|\n".join(linespace.astype(str)))


################################################################
# Notice: len(linespace) have to be greater than 2.
################################################################

# テストデータ 1
print("")
print("================ テストデータ1 ================")
middle_points_of_linespace = np.array([(x2 + x1)/2 for x1, x2 in zip(linespace, linespace[1:])])
print("\n|\n".join(middle_points_of_linespace.astype(str)))

# テストデータ 2 境界値のデータ(関数が境界値でどのような振る舞いをするか調べるために最後に使用する)
print("")
print("================ テストデータ2 ================")
edge_points_of_linespace = linespace[:]
print("\n|\n".join(edge_points_of_linespace.astype(str)))


# 数直線とテストデータの関係(期待値)を表示
print("")
print("================数直線と テストデータ 1 の関係================")
print("\n|\n".join("{}\n|\n(テストデータ{})".format(i, mi) for i, mi in zip(linespace, middle_points_of_linespace)))
print("|\n{}".format(linespace[-1]))

# 変換関数の処理(面倒なので関数化していない)
# テストデータを一つづつ読み込んで、プリントする
print("")
print("================ 検証 テストデータ1 ================")
for v in middle_points_of_linespace:
    # 数値をインデックスに変換する(１行で終わり)
    index = int((v - A) / (B - A) * N)
    # 以下は数値が linespace の範囲外にあった場合の対処
    if index < 0:
        print("変換先がlinespaceのインデックスの範囲外です")
    elif index > len(linespace) - 1:
        print("変換先がlinespaceのインデックスの範囲外です")
    # テストデータの値 と linespace の値の関係を プリントする
    else:
        print("{} < {} < {}".format(linespace[index], v, linespace[index+1]))


# 境界値のテストデータでテストすると予測しにくい動きとなる
print("")
print("================ 検証 テストデータ2 ================")
for v in edge_points_of_linespace:
    # 数値をインデックスに変換する(１行で終わり)
    index = int((v - A) / (B - A) * N)
    # 以下は数値が linespace の範囲外にあった場合の対処
    if index < 0:
        print("変換先がlinespaceのインデックスの範囲外です")
    elif index > len(linespace) - 2:
        print("変換先がlinespaceのインデックスの範囲外です")
    # テストデータの値 と linespace の値の関係を プリントする
    else:
        print("{} < {} < {}".format(linespace[index], v, linespace[index+1]))

出力結果:

================ 数直線 ================
-2.0
|
-1.5
|
-1.0
|
-0.5
|
0.0
|
0.5
|
1.0
|
1.5
|
2.0

================ テストデータ1 ================
-1.75
|
-1.25
|
-0.75
|
-0.25
|
0.25
|
0.75
|
1.25
|
1.75

================ テストデータ2 ================
-2.0
|
-1.5
|
-1.0
|
-0.5
|
0.0
|
0.5
|
1.0
|
1.5
|
2.0

================数直線と テストデータ 1 の関係================
-2.0
|
(テストデータ-1.75)
|
-1.5
|
(テストデータ-1.25)
|
-1.0
|
(テストデータ-0.75)
|
-0.5
|
(テストデータ-0.25)
|
0.0
|
(テストデータ0.25)
|
0.5
|
(テストデータ0.75)
|
1.0
|
(テストデータ1.25)
|
1.5
|
(テストデータ1.75)
|
2.0

================ 検証 テストデータ1 ================
-2.0 < -1.75 < -1.5
-1.5 < -1.25 < -1.0
-1.0 < -0.75 < -0.5
-0.5 < -0.25 < 0.0
0.0 < 0.25 < 0.5
0.5 < 0.75 < 1.0
1.0 < 1.25 < 1.5
1.5 < 1.75 < 2.0

================ 検証 テストデータ2 ================
-2.0 < -2.0 < -1.5
-1.5 < -1.5 < -1.0
-1.0 < -1.0 < -0.5
-0.5 < -0.5 < 0.0
0.0 < 0.0 < 0.5
0.5 < 0.5 < 1.0
1.0 < 1.0 < 1.5
1.5 < 1.5 < 2.0
変換先がlinespaceのインデックスの範囲外です

調べたところ、numpy のライブラリ np.digitize に同様の機能が実装されているようでした。
検証のコードは以下になります。
等号を「a <= b < c」にするか「a < b <= c」にするかは、キーワード引数 right を False か True に設定すると指定できるようです。
（デフォルトでは right=False）
また、範囲外のインデックスは 0 と len(linespace) - 1 のインデックスに変換されるので注意が必要です.

# -*- coding:utf-8 -*-
import numpy as np

# 分割数
N = 8

# 下限
A = -2.0

# 上限
B = 2.0

# 均等に分割した数直線
linespace = np.linspace(A, B, N + 1)

# 数直線を表示

print("================ 数直線 ================")
print("\n|\n".join(linespace.astype(str)))


################################################################
# Notice: len(linespace) have to be greater than 2.
################################################################

# テストデータ 1
print("")
print("================ テストデータ1 ================")
middle_points_of_linespace = np.array([(x2 + x1)/2 for x1, x2 in zip(linespace, linespace[1:])])
print("\n|\n".join(middle_points_of_linespace.astype(str)))

# テストデータ 2 境界値のデータ(関数が境界値でどのような振る舞いをするか調べるために最後に使用する)
print("")
print("================ テストデータ2 ================")
edge_points_of_linespace = linespace[:]
print("\n|\n".join(edge_points_of_linespace.astype(str)))


# 数直線とテストデータの関係(期待値)を表示
print("")
print("================数直線と テストデータ 1 の関係================")
print("\n|\n".join("{}\n|\n(テストデータ{})".format(i, mi) for i, mi in zip(linespace, middle_points_of_linespace)))
print("|\n{}".format(linespace[-1]))

# 変換関数の処理(面倒なので関数化していない)
# テストデータを一つづつ読み込んで、プリントする
print("")
print("================ 検証 テストデータ1 ================")
for v in middle_points_of_linespace:
    # 数値をインデックスに変換する(１行で終わり)
    index = np.digitize(v, linespace)
    print("{} <= {} < {}".format(linespace[index - 1], v, linespace[index]))

# 境界値のテストデータでテストしても問題ないことを確認できる
print("")
print("================ 検証 テストデータ2 ================")
for v in edge_points_of_linespace:
    # 数値をインデックスに変換する(１行で終わり)
    right = False # 右側の等号を有効にする場合はTrue, 左側の等号を有効にする場合は False
    index = np.digitize(v, linespace, right=right)
    # np.digitize は範囲外の値を 0 と len(linespace)-1 に変換するので注意
    # 以下は数値が linespace の範囲外にあった場合の対処
    if index < 1:
        print("{} の変換先がlinespaceのインデックスの範囲外です".format(v))
    elif index > len(linespace) - 1:
        print("{} の変換先がlinespaceのインデックスの範囲外です".format(v))
    # テストデータの値 と linespace の値の関係を プリントする
    else:
        left_eq = "=" if not right else ""
        right_eq = "=" if right else ""
        print("{} <{} {} <{} {}".format(linespace[index - 1], left_eq, v, right_eq, linespace[index]))

出力

 ================ 数直線 ================
-2.0
|
-1.5
|
-1.0
|
-0.5
|
0.0
|
0.5
|
1.0
|
1.5
|
2.0

================ テストデータ1 ================
-1.75
|
-1.25
|
-0.75
|
-0.25
|
0.25
|
0.75
|
1.25
|
1.75

================ テストデータ2 ================
-2.0
|
-1.5
|
-1.0
|
-0.5
|
0.0
|
0.5
|
1.0
|
1.5
|
2.0

================数直線と テストデータ 1 の関係================
-2.0
|
(テストデータ-1.75)
|
-1.5
|
(テストデータ-1.25)
|
-1.0
|
(テストデータ-0.75)
|
-0.5
|
(テストデータ-0.25)
|
0.0
|
(テストデータ0.25)
|
0.5
|
(テストデータ0.75)
|
1.0
|
(テストデータ1.25)
|
1.5
|
(テストデータ1.75)
|
2.0

================ 検証 テストデータ1 ================
-2.0 <= -1.75 < -1.5
-1.5 <= -1.25 < -1.0
-1.0 <= -0.75 < -0.5
-0.5 <= -0.25 < 0.0
0.0 <= 0.25 < 0.5
0.5 <= 0.75 < 1.0
1.0 <= 1.25 < 1.5
1.5 <= 1.75 < 2.0

================ 検証 テストデータ2 ================
-2.0 <= -2.0 < -1.5
-1.5 <= -1.5 < -1.0
-1.0 <= -1.0 < -0.5
-0.5 <= -0.5 < 0.0
0.0 <= 0.0 < 0.5
0.5 <= 0.5 < 1.0
1.0 <= 1.0 < 1.5
1.5 <= 1.5 < 2.0
2.0 の変換先がlinespaceのインデックスの範囲外です

なんか悔しいので timeit を使いスピードを比較してみる。

np.digitize(0, linespace)
455 ns ± 2.48 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)

int((0 - A) / (B - A) * N)
179 ns ± 3.53 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)

結果を見ると
ライブラリ(上): 455 ns
独自手法(下): 179 ns

独自手法は 2.5 倍くらい早い。さらに
ライブラリはバイナリサーチのようなことをやっているらしいので、データが増えるとバイナリサーチはlog関数的に時間がかかるようになるが、独自手法はデータ数に関わらずこの速度を保ち続ける。
まさに数学の勝利である。(ただし境界値の問題を除く)
そういうことなのですが、境界値の問題があるため、おとなしく np.digitize を使うようにしておきます。

以上です。

指数移動平均(ema)について考察する

指数移動平均(Exponential Moving Average 以下 ema)の仕組みや動作がよくわからないので、計算式をPythonで実装し、関数に適用してみます。
emaの計算式は以下のWikipediaのページを参考にしました。

https://en.wikipedia.org/wiki/Moving_average#Exponential_moving_average

これによると、emaの式は以下のように表されるようです。
SとYをtの関数とし、SをYのemaとすると以下のように表せます。

・t = 1 のとき
　S(t) =Y(1)

・t > 1 のとき
　S(t) = a * Y(t) + (1 - a) * S(t-1)

a の取りうる値は 0.0 〜 1.0 で、
ema は　a の値が 1.0 のとき現在の Y(t) の値そのものに、 0.0 のとき Y(0) の値そのものになります。

ここでは、 a の値を変化させたときの ema の値を見てみます。さらに、過去のデータを直近のものに限定した場合のemaの値も見てみます。

ソースコード：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider

def St_a(y):
    return y

def St_b(alpha, St_minus, Yt):
    return alpha * Yt + (1.0 - alpha) * St_minus

def S(alpha, y):
    ret = []
    for i in range(150):
        if i==0:
            ret.append(St_a(y[i]))
        else:
            ret.append(St_b(alpha, ret[i-1], y[i]))
    return ret

N = 3
alpha_0 = 0.5
x = np.arange(150)
y = 2*np.sin(N*2*np.pi/150*x) + np.random.randn(150)
s = S(alpha_0, y)

fig, (ax, ax_slider_1, ax_slider_2) = plt.subplots(3, 1, gridspec_kw = {'height_ratios':[14, 1, 1]})
ax.plot(x, y, linestyle='--')
ax.plot(x, 2*np.sin(N*2*np.pi/150*x), linestyle=':')
ax_s, = ax.plot(x, s)

sldr_1 = Slider(ax_slider_1, 'alpha', 0.0, 1.0, valinit=alpha_0)
sldr_2 = Slider(ax_slider_2, 'start_index', 0, 149, valinit=0, valfmt="%d")

def update_s(alpha_val):
    ax_s.set_xdata(x)
    ax_s.set_ydata(S(alpha_val, y))
    sldr_2.set_val(0)
    fig.canvas.draw_idle()

def update_s_start(s_start_index):
    s_start_index = int(s_start_index)
    tmp_y = y.copy()
    tmp_y[:s_start_index] = tmp_y[s_start_index]
    ax_s.set_xdata(x[s_start_index:])
    ax_s.set_ydata(S(sldr_1.val, tmp_y)[s_start_index:])
    fig.canvas.draw_idle()

sldr_1.on_changed(update_s)
sldr_2.on_changed(update_s_start)
    
plt.show()

実行結果：

xが横軸, yが縦軸です。

オレンジ色の点線はSin波を表しています。
ema を適用する前の オリジナルの関数は,このオレンジ色のSin波にランダムな値を加えたもので、青色の点線です。
それに ema を適用したのが緑色の線になります。

グラフの下にある スライダーの alpha が 数式の a を表しています。
スライダーの start_index は ema の初期値を表しています。このスライダーは過去のデータを直近のものに限定するために使用します。

まず alpha を動かして見ます。
・a = 0 のときは ema はx軸に関係なく常に初期値を維持し続けます。
・a = 1.0 のときは、青い点線と緑色の線が重なりますので、オリジナルの関数と同じになることがわかります。

次に start_index を動かしてみます。
・a = 0.0 にして start_index をプラス方向に動かすと緑色の線がy軸方向に大きく変動することがわかります。
・a = 1.0 にして start_index をプラス方向に動かしても緑色の線がy軸方向に変動することはないことがわかります。
・a = 0.4 にして start_index をプラス方向に動かすと緑色の線がy軸方向に少しだけ変動します。
・a = 0.05 にして start_index をプラス方向に動かすと緑色の線がy軸方向に大きく変動します。

このことから、 a が 1.0 に近ければ 、大雑把にいうと単純移動平均のように動作することがわかりました。
また、start_index を動かした時のグラフの変化を見ると、データ量が少ない場合はa が0に近いと初期値の影響を大きく受けてしまうため、ノイズの除去をして低周波成分を見たいときなどにはデータ量が必要だということがわかりました。そのためema を 単純移動平均と同じような場面で使うときには a を 1.0 に近付けて使うのが良いということがわかりました。emaは同一のシンプルなアルゴリズムでデータ数に関係なく過去の全ての情報を含む値を算出することができるので便利だと思いました。

以上。

TensorFlow で「y=x*(x-1)*(x-2)」の極小値を求める

TensorFlow を利用し関数の局所的に凹になってる箇所ー Local Minima ーすなわち数学的にいう極小値を求めてみようと思います。今回、対象とする関数は 「y = x*(x-1)*(x-2)」です。グラフにすると以下のようになると思います。汚くてすいません。

ちなみにこの関数は x = 1 ± 1/√3 (約1.577, 約0.422)のとき極小値と極大値をとります。極小値と極大値はy=f(x)のグラフの傾きが0となる箇所を求めればよいです。すなわち、関数を微分したものをf'(x)とすればf’(x)=0となるxを求めればよいことになります。試しに Sympy で確かめてみます。

from sympy import Symbol, solve
x = Symbol('x')
y = x*(x-1)*(x-2)
print(solve(y.diff(x)))
# output:
# [-sqrt(3)/3 + 1, sqrt(3)/3 + 1]

Sympy により、すでに答え(x =1.577)は出てしまったのですが、これを TensorFlow を用いて数値計算的に求めることが今回のゴールです。(上記 Sympy の例では 記号的なアルゴリズムで求めていると思われるため今回の TensorFlow で求めるやり方と内部の動きが異なります。)

ここからTensorFlow を用いて最急降下法(Gradient Descent)によって関数の極小値を見つけます。TensorFlow では、最急降下法により関数の極小値を求めるための「TensorFlow.train.GradientDescentOptimizer」クラスとその「minimize」オペレーションが用意されています。今回は、それと同様のオペレーションのある「TensorFlow.train.MomentumOptimizer」クラスを使用し、得られたxとyの値をグラフにプロットし、画像として保存し得られたxとyを見てみます。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# 関数 y = x*(x-1)*(x-2) を定義
def f(x):
    return x * (x - 1.0) * (x - 2.0)

def save_graph(solved_x, filename):
    # グラフ描画して保存
    # x軸とy軸を描画
    plt.axis('off')
    plt.axhline(0, color='black', linewidth=1)
    plt.axvline(0, color='black', linewidth=1)
    # (x, y) = (0, 0) に点を描画
    plt.plot(0, 0, marker='o', color='black')
    plt.text(0, 0, "(0, 0)")
    # (x, y) = (1, 0) に点を描画
    plt.plot(1, 0, marker='o', color='black')
    plt.text(1, 0, "(1, 0)")
    # (x, y) = (2, 0) に点を描画
    plt.plot(2, 0, marker='o', color='black')
    plt.text(2, 0, "(2, 0)")
    # x軸にラベルを追加
    plt.text(2.3 + 0.2, 0, "x", verticalalignment='center')
    # y軸にラベルを追加
    plt.text(0, f(2.3)+0.2, "y", horizontalalignment='center')
    # 関数 y = f(x) を x = [-0.3, 2.3] の範囲で描画
    a = np.linspace(-0.3, 2.3, 100)
    b = f(a)
    plt.plot(a, b, label='y = x*(x-1)*(x-2)')
    plt.legend(loc=1)
    # 極小値の描画
    plt.plot(solved_x, f(solved_x), marker='o', color='orange')
    # f(x)=0 の点をわかりやすくするための線を描画
    plt.axvline(solved_x, linestyle='--', color='orange')
    plt.axhline(f(solved_x), linestyle='--', color='orange')
    plt.text(solved_x, f(solved_x)-0.1, "(x, y)=(%f, %f)"%(solved_x, f(solved_x)), horizontalalignment='center')
    plt.savefig(filename)
    plt.close()


################################################################
# メイン
################################################################
x_kyokusyou = 1.0 - 1.0/np.sqrt(3) # 極大値(local maxima)をとるxの値
#x_start = x_kyokusyou - 0.01 # パターン1
#x_start = x_kyokusyou + 0.01 # パターン2
x_start = 2.2 # パターン3
x = tf.Variable(x_start)

y = x * (x - 1.0) * (x - 2.0)
#grad_opt = tf.train.GradientDescentOptimizer(0.03)
grad_opt = tf.train.MomentumOptimizer(0.01, 0.95)
grad_opt_minimize = grad_opt.minimize(y)
init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    for i in range(200):
        sess.run(grad_opt_minimize)
        solved_x = sess.run(x)
        if solved_x < -0.3: # -infに落ちるので途中でやめる
            break
        # グラフ描画して保存
        save_graph(solved_x, "/Users/kei/Desktop/pic/%03d.png"%i)

初期値を変えて3パターン(パターン1、パターン2、パターン3)で試し、出力されたグラフを動画にしてみました。

・パターン1(初期値 x=1-1/√3 - 0.01)

・パターン2(初期値 x=1-1/√3 + 0.01)

・パターン3(初期値 x=2.2)

パターン1では求めた点がx軸のマイナス方向へ向かって凹があるまで移動していきます。この関数は x < 1 - 1/√3 では凹となる箇所がないため点が無限に移動し続けます。パターン2、パターン3は振り子のように減衰しながら極小値に収束していくように移動します。

最後に、パターン3で求めたxを見て見ます。

print(solved_x)
# output:
# 1.5798204

多少の誤差はありますが、現在の繰り返し回数を200回から増やせば誤差はなくなっていくものと思われます。

以上より、最急降下法によって関数の極小値を数値計算的に求められることがわかりました。
今回の例ではパラメータが一つなため計算量が少なくCPUでもそんなに時間もかからず求まりますが、、ニューラルネットワークの場合は計算量が層の深さの累乗のオーダーで大きくなっていきます。ただ、計算自体は１度、計算式を組み立ててしまえば、その計算式にひたすら数値を代入して演算を繰り返してニューラルネットワークを更新するだけです。そのためGPUのように安く大量の数値計算の並列処理ができるデバイスとこの方法を掛け合わせることによりディープラーニングが実用的なものになり、それが現在の第３次人口知能ブームのきっかけなのではないかと思っています。

以上です。おやすみなさい。